DIVISIBILIDAD

Múltiplos y divisores. 

Criterios de divisibilidad. 

Números primos y compuestos. 

Mínimo común múltiplo y máximo común divisor.

MÚLTIPLOS Y DIVISORES

Dado un múltiplo de un número, siempre es posible encontrar otro múltiplo mayor que él. 

El producto de dos números es múltiplo de cada factor. 

1. Escribe en tu archivador los números que cumplen estas características. 

  • Los múltiplos de 5 que son menores que 48. 
  • Los múltiplos de 9 mayores que 30 y menores que 100. 
  • Los múltiplos de 3 que son impares y están comprendidos entre 31 y 44.

¿Es el número 1 divisor de cualquier otro número? ¿Y de sí mismo? ¿Cuál es el mayor divisor de un número? 

Dado un número, ¿puede ser divisor suyo otro número mayor que él? 

2. HAZ la división y contesta. 104 : 13 ¿Es 13 divisor de 104? • ¿Es 104 divisor de 13? 

 ENCUENTRA tres divisores de cada número. 

  • 45 
  • 80 
  • 144 
  • 25

CRITERIOS DE DIVISIBILIDAD

PENSEMOS ENTRE TODOS

Si un número tiene como divisor a 2, ¿puede ser su última cifra 3? • Si un número es divisible por 2 y por 5 a la vez, ¿se puede decir que es divisible por 10? • Un número es múltiplo de 3. ¿Es 9 su divisor? Si es múltiplo de 9, ¿es divisible por 3? 

Piensa en números que cumplan las siguientes condiciones:

  • Son divisibles por 5 y están comprendidos entre 121 y 148. 
  • Tienen 2 cifras y son divisibles por 3 pero no por 5. 
  • Tienen 3 cifras y son divisibles por 2 y 3 pero no por 5 ni 9. 

3. Escribe dos números de más de cuatro cifras en cada caso. 

  • Divisibles por 2 
  • Divisibles por 3. 
  • Divisibles por 4. 
  • Divisibles por 5. 
  • Divisibles por 6. 
  • Divisibles por 9.
  • Divisibles por 10.

4. En una tienda de especias tienen 1 kg y 250 g de hebras de azafrán. Para su venta, quieren empaquetarlo en cajitas de 1, 2, 3, 5, 9 o 10 g. 

  • Si las cajas fueran iguales, ¿qué tipos de caja pueden utilizar para que no sobre azafrán? 
  • Finalmente, deciden preparar 10 cajitas de 10 g, 20 de 9 g, la mitad del azafrán restante en cajitas de 3 g y la otra mitad en cajitas de 2 g. ¿Es esto posible? ¿Por qué?

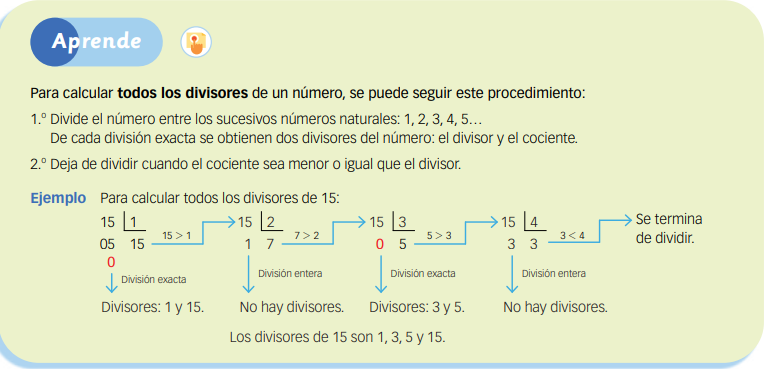
CÁLCULO DE TODOS LOS DIVISORES DE UN NÚMERO

OTRA FORMA...

PIENSA EN COMO OBTENER ESE NÚMERO MULTIPLICANDO OTROS DOS.

¿Es posible escribir todos los múltiplos de un número? ¿Y todos sus divisores? ¿De qué números es divisor el 1? 

A un campamento han ido 60 estudiantes. Formarán grupos con el mismo número de personas para dormir en las tiendas. ¿De cuántas formas pueden agruparse? ¿Cuántas tiendas utilizarán en cada caso? 

DESCOMPOSICIÓN FACTORIAL

1. ¿Qué es la descomposición factorial?

Imagina que un número es como una torre hecha de piezas. La descomposición factorial es desarmar la torre hasta llegar a las piezas más pequeñas que no se pueden dividir más: los números primos.

2. ¿Qué son los números primos?

Son los números mayores que 1 que solo se pueden dividir entre 1 y ellos mismos. Ejemplos: 2, 3, 5, 7, 11, 13…

3. ¿Cómo descomponemos un número?

  • Empezamos dividiendo entre el número primo más pequeño posible (2, 3, 5, 7…).

  • Seguimos dividiendo el cociente hasta que lleguemos a un número primo.

  • Escribimos el número como el producto de esos factores primos.

🔹 Ejemplo visual

Número: 36

  1. 36 ÷ 2 = 18

  2. 18 ÷ 2 = 9

  3. 9 ÷ 3 = 3

  4. 3 ÷ 3 = 1 ✅

36 = 2x2x3x3   ahora escríbelo tú con potencias (operación combinada)

4. Estrategia sencilla

  • Siempre empezamos por el primo más pequeño (2).

  • Si no es divisible, pasamos al siguiente primo (3, luego 5…).

  • Usamos una tabla de factores primos o un árbol de factores para visualizarlo.

💡 MATECONSEJO:

Antes de empezar, pregunta:
"¿Este número es par? ¿Se puede dividir entre 3? ¿Se puede dividir entre 5?"
Esto ayuda a encontrar rápidamente los primeros factores primos.

✏ 5. Ejercicios para practicar

Descompón el número 48 y expresa como producto de sus factores primos.

Descompón el número 72 y expresa como producto de sus factores primos.

Descompón el número 100 y expresa como producto de sus factores primos.

Descompón el número 90 y expresa como producto de sus factores primos.

Descompón el número 150 y expresa como producto de sus factores primos.

💡 Consejo para el niño:

Antes de empezar, pregunta:
"¿Este número es par? ¿Se puede dividir entre 3? ¿Se puede dividir entre 5?"
Esto ayuda a encontrar rápidamente los primeros factores primos.

6.  Descomposición factorial de 84 y 225

Instrucciones:

  1. Divide el número entre el primer número primo posible (2, 3, 5, 7…).

  2. Repite el proceso con el cociente hasta llegar a un número primo.

  3. Escribe la descomposición en forma de producto de números primos.

  4. Finalmente, expresa el resultado con potencias cuando un mismo primo se repita.

Mínimo común múltiplo (M.C.M.) y máximo común divisor (m.c.d.)

7. Realiza estos ejercicios en tu archivador (a, b, c y d)

TOMA RETO! Ejercicio 8, halla el m.c.m y M.C.D. de los números del ejercicio 5,

PROBLEMAS de m.c.m. y M.C.D.

  1. Luces intermitentes
    Una luz parpadea cada 12 segundos y otra cada 18 segundos.
    ¿Cuántos segundos pasarán hasta que vuelvan a parpadear a la vez?

  2. Viajes en autobús
    Un autobús sale de la estación cada 30 minutos y otro cada 45 minutos.
    Si ahora acaban de salir juntos, ¿cada cuánto tiempo volverán a coincidir en la estación?

  3. Repartiendo caramelos
    La seño tiene 48 caramelos de fresa y 60 de limón. Quiere hacer bolsas con la misma cantidad de caramelos y que todas tengan el mismo número de cada sabor.
    ¿Cuál es el mayor número de bolsas que puede hacer?

  4. Saltos en el patio
    En educación física, Pedro salta cada 15 segundos y Ana cada 20 segundos.
    Si empiezan a la vez, ¿cada cuánto tiempo volverán a saltar juntos?

  5. Agrupar alumnos
    En un colegio hay 72 niños y 96 niñas. Se quiere formar grupos con el mismo número de niños y de niñas, sin que sobre nadie.
    ¿Cuál es el mayor número de grupos que se pueden formar?

  6. Campanas
    Una campana suena cada 8 minutos y otra cada 12 minutos. Si suenan juntas a las 12:00, ¿a qué hora volverán a sonar al mismo tiempo?

  7. Repartiendo pizarras
    El colegio compró 54 tizas azules y 81 blancas. Se quieren repartir en cajas iguales sin que sobre ninguna.
    ¿Cuál es el mayor número de cajas que se pueden preparar?

  8. Juegos en la feria
    En una feria, un juego reparte premios cada 14 turnos y otro cada 21 turnos.
    Si ambos coinciden en repartir premio ahora, ¿cada cuántos turnos volverán a coincidir?

  9. Reparto de galletas
    Un niño tiene 84 galletas y otro 126. Quieren guardarlas en bolsas con la misma cantidad en cada una, sin que sobre ninguna.
    ¿Cuántas galletas tendrá cada bolsa si se reparten de la mejor manera?

  10. Ciclistas
    Un ciclista da una vuelta al circuito cada 9 minutos y otro cada 12 minutos.
    Si salen juntos, ¿cuántos minutos tardarán en encontrarse otra vez en la salida?

  11. ALUMNOS DE UN COLEGIO

    El número total de alumnos de un colegio está comprendido entre 200 y 300.
    Cuando los alumnos se colocan en filas de 6, de 8 o de 10, no sobra ninguno. ¿Cuál es el número exacto de alumnos que tiene el colegio? 

👉 En estos problemas:

  • Los que piden máximo número de grupos, bolsas o cajas → se resuelven con M.C.D.

  • Los que piden cuándo coinciden otra vez → se resuelven con m.c.m.

TAREAS DIGITALES

Puedes usar calculadora.

Primera tarea, resolver mcm y MCD. Tiempo máximo 15 minutos. Ojo, recuerda que en la descomposición factorial debes ir por orden de menor a mayor en los números primos (lado derecho de la línea vertical).

www.liveworksheets.com/c?a=s&g=6%C2%BAA&s=MATE_TEMA+2&t=xebu08p9fd&mn=uf&m=d&sr=n&l=rz&i=uxxufo&r=xf&f=dzdfuzzc&ms=uz&cd=pmrfx26h4enxenlsgxmmxejmengnexggkxg&mw=hs

Segunda tarea, resolver mcm y MCD. Sin ayuda visual de la descomposición factorial, puedes hacerla en un folio en sucio.

www.liveworksheets.com/c?a=s&g=6%C2%BAA&s=MATE_TEMA+2&t=xebu08p9fd&mn=uf&m=d&sr=n&l=uj&i=xftcsf&r=jx&f=dzdfuzzc&ms=uz&cd=pmrfx26h4enxenlxqmezkpeqmngnexggkxg&mw=hs

TEST

CUESTIONARIO FINAL TEMA 2

forms.office.com/e/GB0CAKna2s